We have been looking at the stars for too long and have come up with dozens of ideas, laws, and things that we thought governed the universe. Most ideas from the past have become obsolete with new discoveries. However, Johannes Kepler’s three laws for planetary motion have stood the test of time. He created three planetary laws, and today, we will look into Kepler’s third law, the last one.
I have examined the second and compared it to the other two laws in my previous articles. So, today, it is time to look into the last one, Kepler’s Third Law. Johannes Kepler is one of the most revolutionary astronomers and scientists in history. It is important to know these laws to understand how planets and other celestial bodies move.
If you are looking for some astronomy books for beginners that also talk about Kepler's Third Law and also other laws, check out my 5 Best Astronomy Books for Beginners article
Johannes Kepler and His Contributions to Astronomy
Johannes Kepler, a renowned German astronomer and mathematician, was born in 1571 in Weil der Stadt, which is now Germany. Kepler’s observations and groundbreaking theories created the foundation for both that time’s and today’s modern astronomy and revolutionized how we understand the cosmos.
Kepler’s journey into astronomy began when he studied at the University of Tübingen. There, he became deeply influenced by the teachings of his mentor, Michael Maestlin. He introduced him to the theories of Nicolaus Copernicus. Copernicus’ heliocentric model, which placed the Sun at the center of the solar system, challenged the prevailing geocentric view of the time, where Earth was believed to be the center of the universe.
Kepler’s early work focused on the motion of celestial bodies and the mathematical principles governing their movements. In 1609, he published his first major work, “Astronomia Nova,” in which he introduced his first two laws of planetary motion. These laws, later known as Kepler’s First and Second Laws, revolutionized our understanding of how planets move around the Sun.
Discovery of Kepler’s Third Law by Kepler
However, Kepler’s Third Law, published in his work “Harmonices Mundi” in 1619, solidified his place in scientific history. This law, also known as the Harmonic Law or the Law of Periods, established a mathematical relationship between the orbital period and the average distance of a planet from the Sun.
The Third Law paved the way for astronomers to understand the patterns and movements of things in the universe, expanding our knowledge of the universe. It laid the groundwork for Isaac Newton’s laws of motion and universal gravitation’s development, which further advanced our understanding of the laws governing planetary motion.
Today, Kepler’s contributions to astronomy remain foundational. His laws of planetary motion provided a framework for subsequent discoveries and calculations, allowing astronomers to accurately predict the positions and movements of planets, comets, and other celestial objects.
The Basics of Kepler’s Laws of Planetary Motion
Kepler’s Laws of Planetary Motion form the cornerstone of modern astronomy and provide a comprehensive understanding of how planets move within our solar system. Before talking about Kepler’s Third Law, I want to give you a very short glimpse into the basics of all three laws. These laws describe the orbital characteristics of planets, revealing the elegant patterns and relationships that govern their motion.
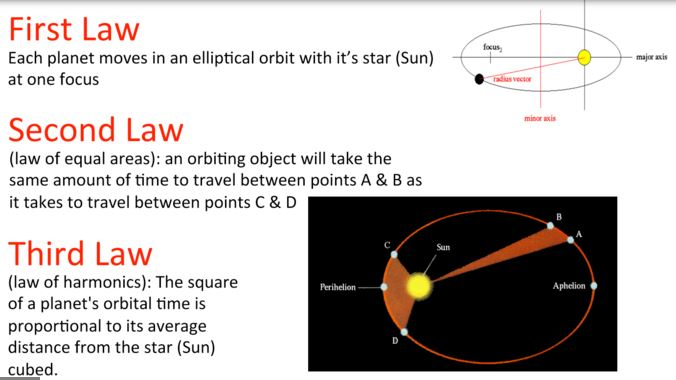
Kepler’s First Law: The Law of Orbits
Kepler’s First Law, also known as the Law of Orbits or the Law of Ellipses, states that the path of each planet around the Sun is an ellipse. This law contradicted the prevailing belief of circular orbits, as proposed by ancient Greek astronomers. The eccentricity of an ellipse determines how elongated or circular an orbit is, with a value of 0 representing a perfect circle and a value closer to 1 indicating a more elongated orbit.
Kepler’s Second Law: The Law of Areas
Kepler’s Second Law, known as the Law of Areas or the Law of Equal Areas, describes the speed at which a planet moves along its elliptical orbit. It states that a line that connects the planet to the Sun takes out equal areas in equal time periods. This means that a planet’s speed increases when it is closer to the Sun and slows down when it is farther away. This law helps explain why planets do not travel at a constant speed throughout their orbits.
Kepler’s Third Law: The Law of Periods
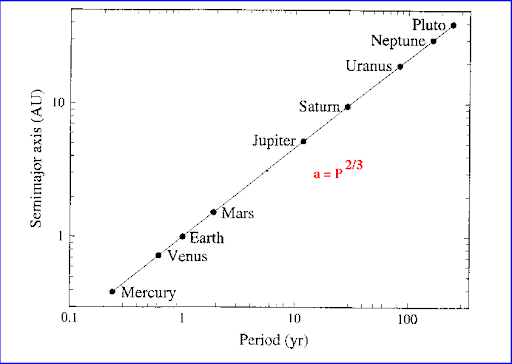
Kepler’s Third Law also referred to as the Law of Periods or the Harmonic Law, establishes a mathematical relationship between the orbital period of a planet and its average distance from the Sun. It basically says that the square of a planet’s orbital period is equal to the cube of its average distance from the Sun. In simpler terms, the more distance a planet has from the Sun, the longer its orbital period.
These three laws, collectively known as Kepler’s Laws of Planetary Motion, provide a comprehensive framework for understanding the motion of planets in our solar system. They elucidate the shape of planetary orbits, the varying speeds of planets along their paths, and the relationship between a planet’s period and its distance from the Sun.
In-depth Understanding of Kepler’s Third Law
The brief mathematical understanding of Kepler’s Law includes the square of a planet’s orbital period, which is T, and the cube of the average distance from the Sun, which is r. Mathematically, it is:
T^2 = k * r^3
T represents the orbital period of the planet, r denotes the average distance between the planet and the Sun, and k is a constant value.

This law implies that planets farther from the Sun take longer to complete one orbit compared to those closer to the Sun. It highlights the inherent harmony and orderliness in the solar system, where the orbital periods and distances of planets follow a predictable pattern.
Applications and Examples of Kepler’s Third Law
Kepler’s Third Law has a lot of applications in the study of the solar system and beyond. By measuring the orbital periods and average distances of planets, astronomers can determine the relative sizes and masses of celestial bodies, even those that are not directly observable.
For example, by applying Kepler’s Third Law, astronomers discovered Neptune, the eighth planet in our solar system. Observations of Uranus revealed discrepancies in its orbital path, suggesting the presence of another gravitational influence. By calculating the expected orbital period and average distance based on the known planets, astronomers predicted the existence and location of Neptune before it was directly observed.
Kepler’s Third Law also allows scientists to estimate the masses of exoplanets (planets outside our solar system) by observing the orbital periods of their host stars and the changes in their brightness as the planets pass in front of them.
Implications and Importance of Kepler’s Third Law
Kepler’s Third Law revolutionized the study of astronomy by providing a mathematical relationship that allows us to understand the motion of planets and other celestial bodies. Here are some of the things Kepler’s Third Law already accomplished.
- Confirmation of the Heliocentric Model. Kepler’s Third Law provided further evidence in support of the heliocentric model proposed by Copernicus. By demonstrating that the orbital periods of planets are related to their distances from the Sun, Kepler’s work reaffirmed the notion that the Sun is indeed the center of our solar system.
- Validation of Newton’s Laws. Kepler’s laws of planetary motion’s crucial data and insights were later incorporated into Newton’s laws of motion and universal gravitation. The relationship between a planet’s orbital period and its distance from the Sun helped to validate Newton’s gravitational theory. This provided a foundation for the understanding of celestial mechanics.
- Basis for Celestial Mechanics. Kepler’s Third Law laid the groundwork for the development of celestial mechanics. This is a branch of astronomy that focuses on the motion of celestial bodies under the influence of gravitational forces. It provided astronomers with a fundamental tool to study the dynamics of planets, moons, comets, and other objects in our solar system.
How It Helps in Understanding Our Solar System
Kepler’s Third Law also has a huge role in helping us understand how our solar system generally works and moves. Here are some of its use cases.
- Determining Planetary Distances. Kepler’s Third Law allows astronomers to determine the average distances between planets and the Sun. By knowing the orbital period of a planet, they can calculate its average distance from the Sun using the mathematical relationship provided by Kepler’s law.
- Estimating Planetary Masses. By combining Kepler’s Third Law with observations of celestial motion, astronomers can estimate the masses of planets. The law allows them to infer the mass of a planet based on its average distance from the Sun and the orbital period.
- Identifying Exoplanets. Kepler’s Third Law has been instrumental in the discovery and characterization of exoplanets. Exoplanets are planets that orbit stars outside our solar system. By observing the periodic variations in a star’s brightness caused by an exoplanet’s transit, astronomers can determine the planet’s orbital period. In turn, this provides valuable information about its distance from the host star.
Modern Uses and Applications
Kepler’s Third Law didn’t stop providing results. It is still in use and helps us quite a lot, even in modern times. We generally use it for three main things, but of course, it is not limited to these.
- Exoplanet Hunting. Kepler’s Third Law is utilized in the search for exoplanets. Astronomers analyze the light curves of stars to identify periodic variations that may indicate the presence of orbiting planets. By leveraging the law’s mathematical relationship, they can estimate the orbital periods of these exoplanets and gain insights into their characteristics.
- Spacecraft Trajectories. In space exploration missions, Kepler’s Third Law is employed to plan spacecraft trajectories. By understanding the relationship between the orbital period and distance, scientists can calculate the necessary velocities and trajectories to reach specific destinations within our solar system.
- Gravitational Wave Detection. Kepler’s Third Law plays a role in the detection and analysis of gravitational waves. These waves, ripples in the fabric of spacetime caused by massive celestial events, provide valuable information about the objects involved. By incorporating Kepler’s law, scientists can estimate the masses and distances of the celestial bodies responsible for generating gravitational waves.
Common Misunderstandings and Clarifications of Kepler’s Third Law
Kepler’s Third Law, while a fundamental principle in understanding planetary motion, can sometimes be subject to common misunderstandings. I will try to show you what those misunderstandings are and what is the correct interpretation of it.
- Misconception: All planets have the same orbital period.
- Clarification. Kepler’s Third Law states that there is a relationship between a planet’s orbital period and its average distance from the Sun. However, this does not imply that all planets have the same orbital period. Each planet has a unique combination of distance and period, resulting in different orbital characteristics.
- Misconception: Kepler’s Third Law works only for planets in our solar system.
- Clarification. Kepler’s Third Law was derived based on observations of our solar system, but it applies to any planetary system. The law holds true for exoplanets orbiting other stars as well. So, it is not just for our solar system. It allows astronomers to estimate their orbital periods and how far away they are from their host stars.
- Misconception: The Law of Periods applies only to planets.
- Clarification. Kepler’s Third Law can be applied to any object orbiting a central body, not just planets. It can be used to study the motion of moons, asteroids, and even human-made satellites around a planet or a star.
Conclusion
Kepler’s Third Law, the Law of Periods, has stood the test of time as a fundamental principle for planetary motion. The long-lasting relevance of Kepler’s Third Law lies in its ability to provide insights to our solar system. When we understand a planet’s orbital period and its estimated distance from the Sun, we can have a deeper understanding of the complicated patterns and harmonies that govern celestial movement.
Kepler’s Third Law not only confirmed the heliocentric model proposed by Copernicus. It also provided a mathematical foundation for the development of celestial mechanics. It played a crucial role in the validation of Newton’s laws of motion and universal gravitation. This paved the way for a profound understanding of the forces that shape our universe.
However, it is important to recognize the limitations and complexities of Kepler’s Third Law. Real-world situations can introduce deviations from the idealized predictions, such as gravitational interactions with other objects or variations in orbital behavior. These factors remind us of the dynamic and complex nature of the universe we inhabit.
Nonetheless, Kepler’s Third Law remains a cornerstone of astronomical research and exploration. Its mathematical relationship continues to guide our understanding of planetary motion and serves as a vital law in solving the mysteries of the cosmos.
FAQ
What is Kepler’s third law simple?
Kepler’s third law is like a rule for planets. It says that if you know how far a planet is from the Sun, you can figure out how long it takes for the planet to go one full circle around the Sun. The further away the planet is from the Sun, the longer it takes to complete one orbit. So, planets that are far from the Sun move slower than the ones closer to the Sun.
What is the constant in Kepler’s third law?
The “constant” in Kepler’s third law is like a magic number that connects the time a planet takes to go around the Sun and how far it is from the Sun. This constant can change depending on what two things are orbiting each other. For example, when we talk about planets going around the Sun, the Sun is so much bigger than any planet that we can kind of ignore the planet’s weight, and the constant stays the same for all planets. But if we were talking about the Moon going around the Earth, then the Earth and the Moon’s weights both matter, so the constant would be different.
What are the names of Kepler’s three laws?
Kepler’s First Law is The Law of Orbits, Kepler’s Second Law is The Law of Equal Areas, and the third one, Kepler’s Third Law, is The Law of Periods.