Humans have been watching space since the beginning of modern history, wondering what is up there. In recorded history, we see a lot of astronomers from the beginning of time. The most significant ones have brought us a better understanding of the space. One of them is Johannes Kepler, founder of Kepler’s second law. What is Kepler’s Second Law, and what do we use it for?
Kepler has three laws that perpetrate the planetary motion. Among Kepler’s three laws, the second law holds a particular significance. It sheds light on the dynamics of orbiting bodies. In this post, our topic will be Kepler’s Second Law. I will try to explain what is Kepler’s Second Law, what it does, and everything related to it.
Introduction to Kepler and His Laws of Planetary Motion
We can’t fully understand Kepler’s Second Law without first understanding the man behind it and his broader contributions to astronomy. Johannes Kepler, a German mathematician, astronomer, and astrologer, lived from 1571 to 1630. He is best known for his three laws of planetary motion. These laid the foundation for our modern understanding of how planets move around the Sun.
Kepler’s laws were a result of meticulous observations and mathematical calculations. They were based on the data collected by his predecessor, Tycho Brahe. Kepler’s work not only challenged the prevailing geocentric model. It also opened the way for Isaac Newton’s laws of motion and universal gravitation.
The three laws of planetary motion devised by Kepler are:
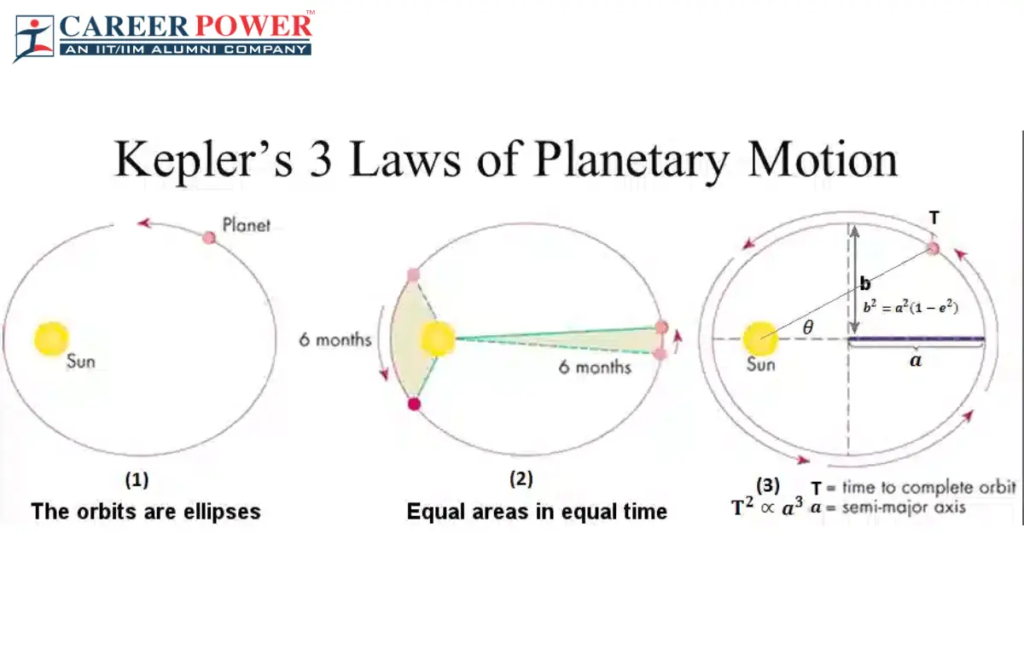
- Kepler’s First Law (The Law of Ellipses). It states that planets move in elliptical orbits with the Sun at the focus.
- Kepler’s Second Law (The Law of Equal Areas). The Second Law, which is our focus today, says that a line segment joins a planet as it moves along its orbit, and the Sun takes out equal areas at equal times.
- Kepler’s Third Law (The Harmonic Law). The last law derived from Kepler’s laws is the third one. It says that the square of the orbital period of a planet stays the same as the cube of the semi-major axis of its orbit.
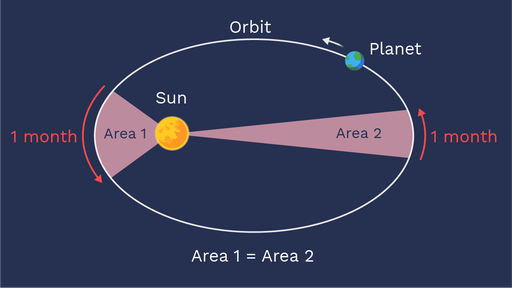
What is Kepler’s Second Law?
Kepler’s Second Law, also known as the Law of Equal Areas, says that a line segment that connects a planet to our Sun takes out the same amount of area in the same time intervals as the planet moves along its elliptical orbit. In simpler terms, it means that any planet moves slower when it is close to the Sun and faster when it is closer to the Sun. This results in an equal area being swept out in equal time intervals.
The Importance of Kepler’s Second Law
Kepler’s Second Law establishes the relationship between the speed of a planet and its distance from the Sun. This is one of the most fundamental things in cosmology and astronomy. That is, to understand the speed of the astronomical bodies relative to their position. That’s how we know how old the space is, for example. Mainly, this law helps us understand how planets travel around their central star.
What’s important is that Kepler’s Second Law challenges the prevailing notion that planets move at a constant speed in their orbits. Instead, it reveals that the motion of celestial bodies is dynamic, and the central object’s forces influence the varying gravitational forces.
All this shows that Kepler’s Second Law can give us a deeper understanding of the complex dance of planets around their host stars. So, this is not just applicable to Earth and the Sun. It applies to all planets with host stars (there are rare planets without host stars, but that is another topic).
The Mathematical Explanation of Kepler’s Second Law
Okay, in normal human terms, Kepler’s Second Law is above. It helps us determine the speed at which a planet travels around its host stars. But how about in nerdy terms, like in real mathematical terms? There is a deep explanation for that, but I will keep it short and neat.
The Mathematical Formula
Kepler’s Second Law can be mathematically expressed using the concept of angular momentum. Angular momentum is the result of an object’s moment of inertia and its angular velocity. In the case of planetary motion, the moment of inertia is proportional to the mass of the planet, and the angular velocity is related to the planet’s orbital speed.
The mathematical expression of Kepler’s Second Law is:
[ \frac{{dA}}{{dt}} = \frac{{1}}{{2}}r^2\frac{{d\theta}}{{dt}} ]
Where:
- (\frac{{dA}}{{dt}}) represents the rate of change of the area swept out by the line segment connecting the planet to the Sun.
- (r) represents the distance between the planet and the Sun.
- (\frac{{d\theta}}{{dt}}) represents the rate of change of the angle between the line segment and a reference direction.
This formula implies that the rate at which the area is swept out is constant, regardless of the distance from the Sun. When a planet is closer to the Sun, it covers a smaller distance in a given time, resulting in a higher orbital speed. Conversely, when the planet is farther away, it covers a larger distance at the same time, resulting in a slower orbital speed.
Understanding the Mathematical Concepts
With the mathematical formula of Kepler’s Second Law, you must understand the concepts of area conservation and the relationship between distance and speed. The concept of area conservation refers to the fact that the area swept out by a planet in a specific time interval remains constant, regardless of its position in its orbit.
The relationship between distance and speed is derived from the conservation of angular momentum. When a planet is closer to the Sun in its elliptical orbit, its distance from the Sun decreases, which leads to a smaller radius ((r)) in the equation. To maintain the constant angular momentum, the planet’s orbital speed ((\frac{{d\theta}}{{dt}})) must increase.
Relative to that, as the planet moves farther from the Sun, its distance increases, resulting in a larger radius ((r)) in the equation. To maintain the constant angular momentum, the planet’s orbital speed ((\frac{{d\theta}}{{dt}})) must decrease.
Applications of Kepler’s Second Law
Determining Planetary Positions and Orbits
Kepler’s Second Law allows astronomers to determine the positions and orbits of planets accurately. By observing the rate of a planet’s speed that sweeps out equal areas in equal time intervals, scientists can calculate the planet’s distance from the Sun at any given time. This information is crucial for constructing accurate models of the solar system and understanding the dynamics of planetary motion.
Studying Exoplanets
Kepler’s Second Law has also been instrumental in the study of exoplanets, planets that orbit stars outside our solar system. By analyzing the light curves of distant stars, astronomers can detect the slight dimming that an exoplanet causes when it is passing in front of its host star. Kepler’s Second Law helps determine the orbital periods and sizes of these exoplanets, providing valuable insights into the diversity and distribution of planetary systems in the universe.

Effects on Satellite Orbits
The law has significant implications for satellite orbits as well. Satellites, such as those used for communication, weather monitoring, and navigation, follow elliptical orbits around the Earth. Understanding it is crucial for properly designing and maintaining these satellite orbits.
Satellite Speed and Coverage
Satellites in higher orbits, where they are farther from the Earth, move at slower speeds due to the larger radius. This slower speed allows them to provide continuous coverage over a particular region of the Earth’s surface, as they take longer to complete each orbit. Satellites in lower orbits, on the other hand, move at higher speeds, providing more frequent coverage but for smaller areas.
Orbital Stability
With this law, we can also ensure the stability of satellite orbits. By maintaining a constant rate of area swept out, satellites can maintain consistent angular momentum, which prevents their orbits from decaying or drifting significantly over time.
Common Misconceptions about Kepler’s Second Law
Misconceptions can often arise when interpreting scientific concepts, and Kepler’s Second Law is no exception. Understanding these misconceptions can help you gain a better understanding of how the Second Law is different from other laws.
Misconception: Equal Time Intervals
One common misconception about Kepler’s Second Law is the assumption that equal time intervals correspond to equal areas swept out. However, this is not the case. The Second Law states that the rate at which the area is swept out is equal. In other words, the planet will sweep out the same amount of area in a given amount of time, but the time intervals themselves may not be equal.
Misconception: Constant Speed
Another misconception is the belief that Kepler’s Second Law implies that the planet moves at a constant speed throughout its orbit. While the law does describe the relationship between a planet’s speed and its distance from the Sun, it does not imply a constant speed. In fact, the planet’s speed varies throughout its elliptical orbit, with higher speeds when it is closer to the Sun and lower speeds when it is farther away.
Common Errors in Application
Just like misunderstandings, there are also misapplications. This implies that we either use or try to use The Second Law in the wrong places. These misapplications could give us extremely wrong results, or it might not work at all.
Misapplication: Circular Orbits
One common error is the application of The Second Law to circular orbits. Kepler’s Second Law specifically applies to elliptical orbits, where the distance between the planet and the Sun changes. In the case of perfectly circular orbits, the distance remains constant, and therefore, the equal area rule does not apply.
Misapplication: Non-Planetary Orbits
Kepler’s Second Law is not limited to planetary orbits alone. It applies to any object in an elliptical orbit around a central body, such as satellites or comets. The law describes the relationship between the rate at which an area is swept out and the distance traveled, regardless of the specific object involved.
Conclusion
In essence, Kepler’s Second Law shows how planets move in space. Kepler’s Second Law reveals that planets’ speed increases or decreases when they are close or farther away from the Sun, creating equal areas in their orbits over time. Beyond planets, this law helps with satellites and understanding other stars and their planets. Basically, what Kepler’s Secon Law is is that it helps us understand the movements of planets relative to the Sun, and they unveil a cosmic ballet, where each orbit tells a story of motion and marvel.
FAQ
What does Kepler’s Second Law follow?
Kepler’s Second Law follows the Law of Ellipses, which is Kepler’s First Law of Planetary Motion. This law says that planets move in oval orbits around the Sun when the Sun is one of the two focuses of the ellipse.
What is Kepler’s Second Law in real life?
In real life, Kepler’s Second Law, also known as the Law of Equal Areas, describes how planets move in their orbits around the Sun. It states that when a planet orbits around the Sun, it will sweep out equal areas in equal periods of time. This means that planets’ speed changes depending on whether they are close or farther away from the Sun, resulting in an equal area being covered in the same amount of time.
What is conserved in Kepler’s Second Law?
In Kepler’s Second Law, the quantity that is conserved is the rate at which area is swept out by a line segment connecting the planet to the Sun. This means that regardless of where the planet is in its orbit, the rate at which it sweeps out area remains constant over time.