How the celestial bodies move out in space depends on certain fundamental laws. We call these laws Kepler’s Laws of Planetary Motion, and there are exactly three of them. Each has its own significance in the governance of the movement of celestial bodies. However, Kepler’s Second Law of Planetary Motion is probably the most important.
Each of these laws is connected to each other, and they differ in how they measure certain things. If you are interested in Kepler and his amazing works, you must understand all and can compare all three to each other. In this article, I am going to take Kepler’s Second Law of Planetary Motion as the center and compare it to the other two Kepler Laws.
Introduction to Kepler’s Laws of Planetary Motion
Kepler’s Laws of Planetary Motion are three cosmological principles that describe the motion of planets and other celestial bodies in our solar system. The famous astronomer and German mathematician Johannes Kepler formulated these laws in the early 17th century. Kepler’s groundbreaking work revolutionized our understanding of planetary motion and paved the way for future advancements in astronomy.
Kepler’s Laws of Planetary Motion were a significant departure from the geocentric model we were following. The geocentric model placed Earth at the center of the universe. Kepler’s laws provided a heliocentric perspective, with the Sun at the center, and laid the foundation for Isaac Newton’s later work on universal gravitation.
Kepler’s First Law (Law of Ellipses)
The first law says that planets do not move in perfect circles or orbits. They rather follow elliptical paths around the Sun, which is at the center. It means a planet’s orbit around the Sun is an ellipse, with the Sun located at one of the ellipse’s two foci.
Kepler’s Second Law (Law of Equal Areas)
The second law states that a planet and its Sun sweep out equal areas in equal time intervals. This essentially says that any planet with a sun moves faster when it is closer to the Sun. Equally, it moves slower when it is farther away, resulting in an equal area being covered in equal time.
Kepler’s Third Law (Harmonic Law)
The last law, the Third law, establishes a mathematical relationship between the orbital periods and average distances of planets from the Sun. It says that a planet’s orbital period is directly related to its semi-major axis cube. It provides a quantitative, rather mathematical, understanding of a planet’s distance from the Sun and its orbital period.
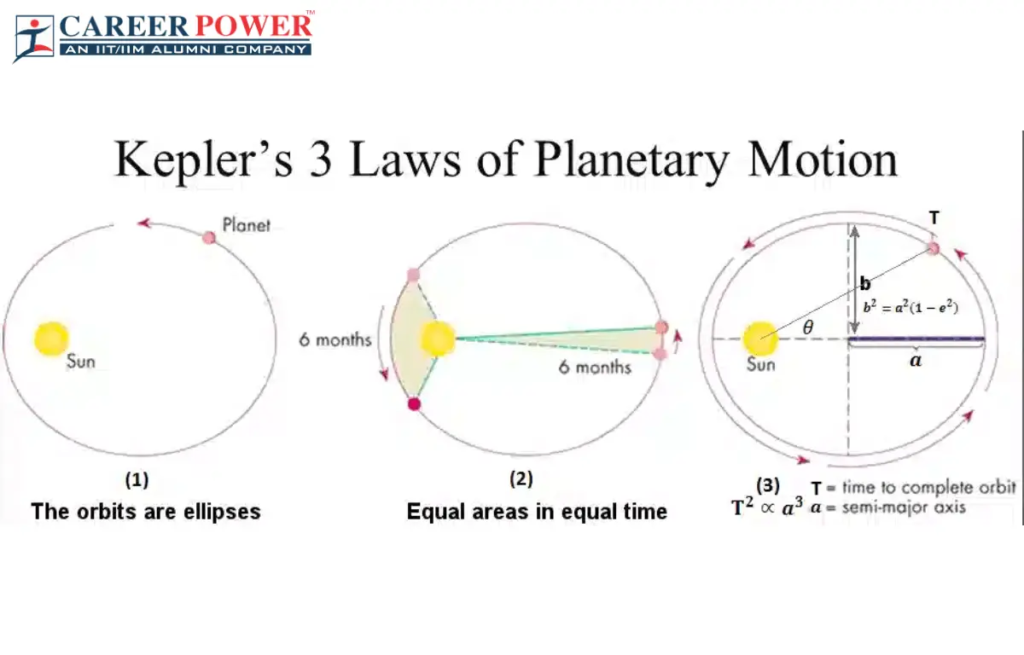
Overview of Kepler’s Second Law
Kepler’s Second Law, also known as the Law of Equal Areas, gives the main insight into the dynamics of planetary motion. It follows the concept of equal areas in equal time in the motion of planets. Kepler’s first and third laws focus on planets’ orbit around the run. The Second Law mostly focuses on the speed of the movements of the planets around the Sun.
The Concept of Equal Areas Equal Time
Kepler’s Second Law basically says that the movement of a planet around its Sun sweeps out equal areas in Sunal time intervals. But what exactly does this mean?
Imagine a planet moving in its elliptical orbit around the Sun. As the planet travels aloSunits path, it sweeps out a wedge-shaped area between the planet-Sun line and the corresponding area it sweeps in a subsequent time interval of equal length. Surprisingly, Kepler discovered that regardless of where the planet is in its orbit, the areas covered in equal time intervals are always equal.
We can visualize this concept by considering a hypothetical planet orbiting the Sun. As the planet gets closer to its Sun, it covers a larger distance in a given time and it results a greater area being swept out. Conversely, when the planet is farther away from the Sun, it covers a smaller distance, resulting in a smaller area being swept out. However, the time taken to sweep out these areas remains constant, ensuring that they are always equal.
How Kepler’s Second Law Applies to Planetary Motion
Kepler’s Second Law, different from the other two Kepler Laws, creates implications for understanding the motion of planets in our solar system. It reveals that a planet’s speed is not constant throughout its orbit but varies depending on its distance from the Sun.
When a planet gets close to its Sun, the Sun’s gravitational pSun gets stronger towards the planet, causing it to accelerate and move at a higher speed. As a result, it covers a larger distance each time, sweeping out a greater area. In reverse, when the planet is farther away from the Sun, the gravitational force causes the planet to decelerate and move at a slower speed. That way, it covers a smaller distance in the same time interval. It results in a smaller area being swept out.
This phenomenon of varying speed is responsible for the asymmetrical shape of a planet’s orbit. The planet spends less time in the farthest regions of its orbit, where it moves slowly, and more time in the closest regions, where it moves faster. As Kepler’s Second Law says, this unequal distribution of time and speed leads to the equal areas being swept out in equal time intervals.
Comparing Kepler’s Second Law of Planetary Motion to Other Laws of Planetary Motion
While fascinating, Kepler’s Second Law of Planetary Motion gains further significance when we compare or use it with the other two laws formulated by Johannes Kepler.
Comparison with Kepler’s First Law
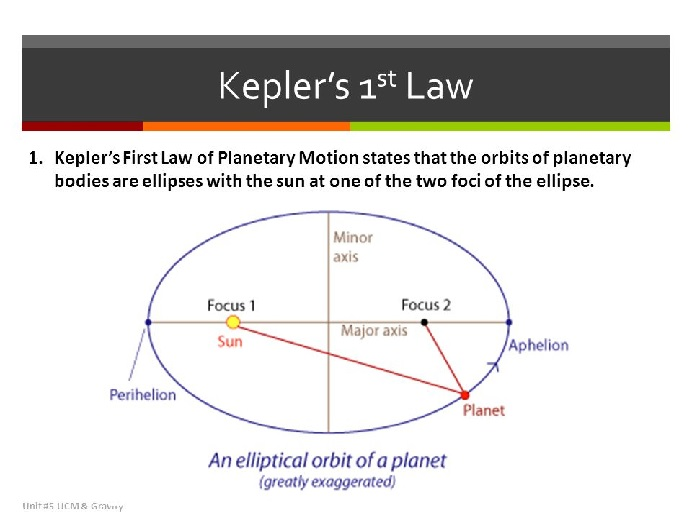
Kepler’s First Law, also known as the Law of Ellipses, says a planet’s orbit around the Sun is an ellipse. The Sun is located at one of the two foci of the ellipse. In contrast, Kepler’s Second Law focuses on the equal areas swept out by the planet in equal time intervals.
While Kepler’s First Law describes the shape of the orbit, Kepler’s Second Law provides insights into the dynamics of planetary motion within that elliptical orbit. The concept of equal areas in equal time reveals the varying speeds of a planet along its path. It shows the relationship between the planet’s distance from the Sun and its orbital speed.
In essence, Kepler’s First Law sets the stage for Kepler’s Second Law, defining the shape of the orbit, while Kepler’s Second Law adds depth by explaining the equal areas in equal time phenomenon.
Comparison with Kepler’s Third Law of Planetary Motion
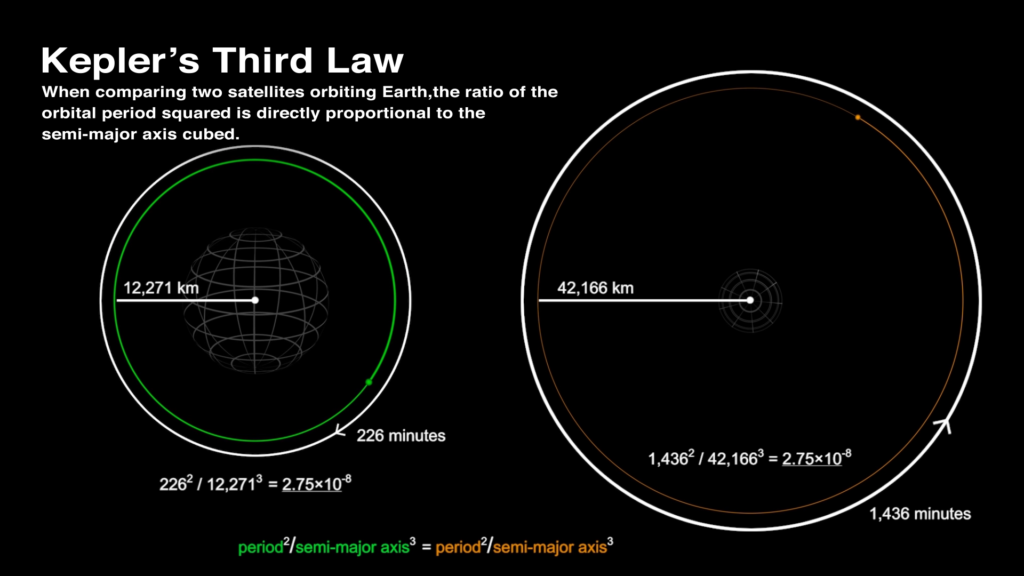
Kepler’s Third Law, also known as the Harmonic Law, establishes a mathematical relationship between the orbital periods and average distances of planets from the Sun. It tells us that the square of the orbital Suniod of a planet is proportional to the cube of its semi-major axis.
Kepler’s Third Law provides a quantitative meaning between a planet’s orbital period and its distance from the Sun. However, Kepler’s Second Law offers insight into the dynamics of planetary motion within that orbit. By understanding the concept of equal areas in equal time, we gain a deeper understanding of the planet’s varying speeds, which directly influence the time taken to complete an orbit.
Kepler’s Second Law and Kepler’s Third Law work together to provide a comprehensive understanding of planetary motion. The combination of these laws allows us to determine not only the shape and size of an orbit but also the dynamics of a planet’s motion within that orbit.
How Kepler’s Laws Interact
Kepler’s Three Laws of Planetary Motion are interconnected and mutually supportive. Kepler’s First Law defines the shape of the orbit, Kepler’s Second Law explains the equal areas in equal time phenomenon, and Kepler’s Third Law establishes a mathematical relationship between the orbital periods and average distances of planets.
Together, these laws form a cohesive framework for understanding how planets and other celestial bodies move in our solar system. They provide us with a deeper appreciation of the intricate dynamics at play, allowing us to make accurate predictions, design spacecraft trajectories, and further our understanding of the universe.
Conclusion
All in all, Kepler’s Planetary Laws explain how they move and how they change. They all support each other in understanding the other Kepler Law. Kepler’s Secondary Law of Planetary Motion, though, is probably one of the most important ones.
Imagine the universe as a dance floor, with planets swirling around the Sun like dancers in a celestial waltz. In this cosmic dance, Kepler’sSunws of Planetary Motion are the ultimate choreographers, guiding each planet’s graceful moves. Among them, Kepler’s Second Law steals the spotlight, revealing the secrets of planetary speed. It’s like the rhythm that keeps the dance in sync, showing us how planets speed up and slow down as they orbit the Sun.
But it’s not just about the moves; it’s about the whole cosmic world working together. Kepler’s laws, like a stellar band, play in perfect harmony, guiding us through the cosmic concert of the universe.
FAQ
What is Kepler’s 2nd law of planetary motion?
Kepler’s Second Law of Planetary Motion, also known as the Law of Equal Areas, describes how a planet moves around its Sun. This means that any planet’s speed increases when it’s close to iSunSun and decreases when it’s farther away. This law helps us understand the dynamics of planetary motion and how the speed of a planet changes as it orbits the Sun.
What is Kepler’s 2nd law described as?
Kepler’s Second Law of Planetary Motion is described as the Law of Equal Areas. Because the law supports the idea that a planet and its Sun sweep out equal areas in equal time intervals as the planet moves along its elliptical orbit around the Sun.
Are Kepler laws accurate?
Yes, Kepler’s laws of planetary motion are highly accurate. Johannes Kepler formulated these laws based on extensive observations made by Tycho BrSun, and they accurately describe how planets move in our solar system. These laws laid the foundation for our modern understanding of planetary motion and have stood the test of time, remaining fundamental principles in the field of astronomy. While they are not perfect due to factors like the gravitational interactions with other celestial bodies and relativistic effects, Kepler’s laws provide an excellent framework for predicting and understanding planetary motion.