Entropy is a fundamental concept in physics. This theory has a crucial role in understanding the behavior of systems at various scales. This includes microscopic particles and the entire universe. It is often difficult to understand, but the importance of entropy cannot be overstated. In this blog post, we will explore entropy and its applications in different branches of physics. These include thermodynamics, statistical mechanics, and quantum mechanics.
If you are interested in physics or want to learn more about how the universe works, this explanation of entropy will introduce you to the basic principles that control our physical reality.
Introduction to Entropy
Entropy is a fundamental concept that has intrigued and puzzled scientists for centuries. It helps us understand the behavior of systems, from simple to complex, in fields such as thermodynamics, statistical mechanics, and quantum mechanics.
First off, what is Entropy? Entropy is a concept that started in physics but we use it widely across various fields. It fundamentally refers to the measure of disorder or randomness in a system.
Think of a deck of cards. When we sort all the cards in order by suit and number, it’s very organized, right? The entropy here is low because it’s highly ordered. If you throw the cards randomly, they’re all jumbled up – that’s high entropy. Essentially, entropy quantifies the randomness or unpredictability in the arrangement of the cards.
In the natural world, entropy often tends to increase over time. Take an ice cube melting into water. The molecules are organized and structured in the solid form, so there’s low entropy. As it melts into liquid, the molecules move more randomly, leading to higher entropy.
Entropy is also tied to the concept of probability and information theory. In information theory, lower entropy implies predictability, while higher entropy means more uncertainty and randomness. For instance, in a simple sequence of coin tosses, getting alternating heads and tails is less probable than getting a random mix of heads and tails, showing higher entropy in the latter case.
Overall, entropy is a measure of disorder, randomness, or unpredictability in a system, whether it’s about the arrangement of particles, energy distribution, or the likelihood of events occurring.
Origins of the Concept
The German physicist Rudolf Clausius introduced the concept of entropy in the mid-19th century. Clausius coined the term “entropy” from the Greek word “entropia,” which means “transformation” or “turning inside out.” He recognized that there was a fundamental connection between heat transfer and the irreversibility of certain processes.
Entropy and Energy
Entropy is related to the concept of energy. In a system with high entropy, the energy is distributed more disordered and less usable. Conversely, in a system with low entropy, the energy is more concentrated and available for useful work.
The Entropy Change
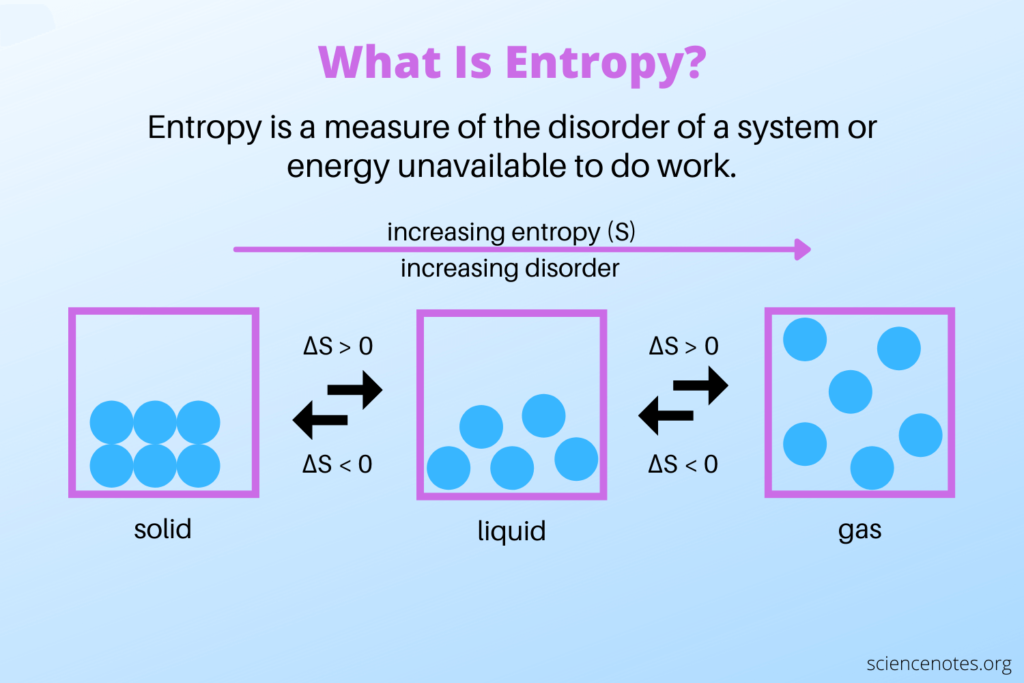
Entropy change, denoted as ΔS, is a measure of the change in entropy between two states of a system. Its value could be positive, negative, or zero. It depends on the nature of the process. An increase in entropy (ΔS > 0) indicates an increase in disorder, while a decrease in entropy (ΔS < 0) indicates a decrease in disorder or an increase in order.
Entropy and the Second Law of Thermodynamics
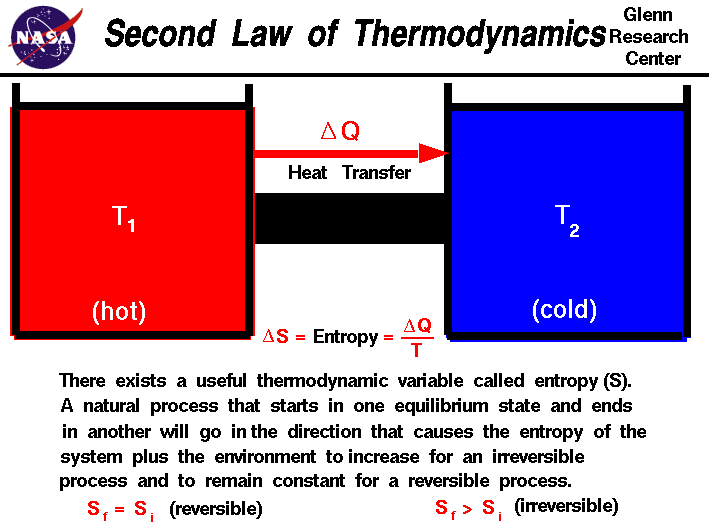
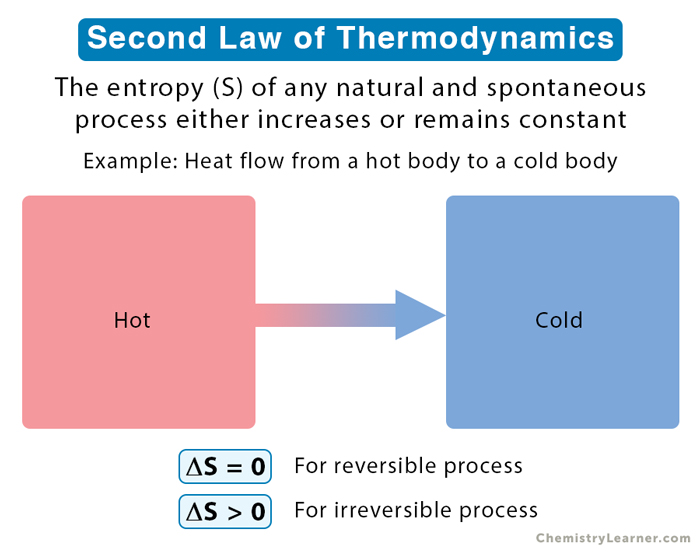
Entropy is highly related to the second law of thermodynamics. This law says that the entropy of an isolated system generally increases over time or, at best, remains constant in reversible processes. The principle that the entropy of the universe always increases is quite famous.
We have also linked Entropy to information theory, which measures the amount of uncertainty or randomness in a data set. The higher the uncertainty or randomness of the data, the higher the entropy.
The Concept of Entropy in Thermodynamics
In thermodynamics, entropy is a key concept that helps us understand the behavior and transformations of energy in systems. This section will provide a comprehensive understanding of entropy within the context of thermodynamics.
Definition and Basic Understanding
Entropy in thermodynamics measures the system’s unavailability of energy to do work. It is denoted by the symbol S and is a state function, meaning it depends only on the system’s current state and not on the path taken to reach that state.
To understand entropy, it is important to recognize that it is related to the energy distribution within a system. A highly ordered and organized system will have low entropy. Conversely, a system with a more disordered and spread-out energy distribution will correspond to high entropy.
The Second Law of Thermodynamics
The second law of thermodynamics governs the behavior of entropy. It states that the total entropy of an isolated system will always increase over time or remain constant in reversible processes. This law implies that processes tend to move towards a state of higher entropy, leading to an overall increase in disorder and randomness in the universe.
Entropy and Energy Distribution
Entropy is closely linked to how energy is distributed within a system. Energy is dispersed in systems with high entropy and less available for useful work. This is because the energy is spread out over many microstates, making extracting useful work from the system difficult.
In contrast, systems with low entropy have energy concentrated in a more organized and usable way, making it more readily available for work. For instance, a gas compressed in a cylinder has low entropy. This is because the energy is concentrated in a small volume, which allows it to perform work when released.
Entropy and Heat Transfer
Entropy is also closely related to the process of heat transfer. When heat is transferred from a higher temperature region to a lower temperature region, the entropy of the system increases. This is due to the increase in the number of microstates available to the system as the energy becomes more spread out.
Conversely, when heat is transferred from a lower temperature region to a higher temperature, the entropy of the system decreases. This is because the energy becomes more concentrated, resulting in a decrease in the number of microstates.
Entropy in Statistical Mechanics
In the realm of statistical mechanics, entropy takes on a different perspective. It is no longer merely a macroscopic concept but rather a statistical measure of the underlying microscopic behavior of particles within a system.
Boltzmann’s Equation
In statistical mechanics, entropy is quantitatively described by Boltzmann’s equation. This equation relates entropy (S) to the number of microstates (W) associated with a particular macrostate of a system. The equation is given by:
S = k ln W
where k is the Boltzmann constant, which relates the macroscopic scale to the microscopic scale.
Boltzmann’s equation provides a mathematical framework for understanding the relationship between entropy and the multiplicity of microstates that correspond to a given macrostate. It highlights the probabilistic nature of systems and how the number of possible microscopic arrangements contributes to the overall entropy.
The Microscopic View of Entropy
In statistical mechanics, entropy is viewed from a microscopic perspective. It considers the individual particles or constituents that make up a system. The entropy of a system is a measure of the uncertainty or lack of knowledge about the exact microscopic state of the system.
Since we cannot precisely track the position and momentum of every particle in a macroscopic system, statistical mechanics provides a statistical framework to describe the behavior of the system. Entropy arises from the inherent probabilistic nature of the system, where the exact state of each particle is uncertain.

Entropy and Probability
The entropy in statistical mechanics is intimately connected to the concept of probability. The entropy of a system is related to the likelihood or probability of a particular macrostate occurring. Macrostates with a higher number of associated microstates have a higher probability and, thus, a higher entropy.
The relationship between entropy and probability can be understood through the concept of equilibrium. In an equilibrium state, the system tends to maximize its entropy by exploring all possible microstates with equal probability. This leads to a state of maximum disorder and randomness corresponding to maximum entropy.
Entropy in Quantum Mechanics
Entropy in quantum mechanics introduces a fascinating and unique perspective on the concept. In this section, we will explore how entropy is understood and quantified within the framework of quantum mechanics.
Von Neumann Entropy
In quantum mechanics, entropy is often quantified using Von Neumann entropy. Named after the mathematician John von Neumann, this entropy measures the amount of information and uncertainty present in a quantum system.
Von Neumann entropy is calculated based on the density matrix, which describes the quantum state of a system. By analyzing the eigenvalues of the density matrix, we can determine the entropy of the system. Higher entropy indicates greater uncertainty and information content within the quantum state.
The Role of Entropy in Quantum Information Theory
Quantum information theory explores the transmission, storage, and processing of information in quantum systems. Entropy plays a crucial role in this field, quantifying the information contained within a quantum state.
Entropy is used to measure the purity or mixedness of a quantum state. A pure state has zero entropy, indicating complete knowledge and certainty about the quantum system. On the other hand, a mixed state, which contains a combination of different quantum states, has non-zero entropy, representing the presence of uncertainty and information.
Quantum Entanglement and Entropy
Quantum entanglement is a phenomenon where two or more particles become correlated in a way that a particle’s state cannot be described independently of the other and is closely related to entropy. Entanglement entropy measures the entanglement between different parts of a quantum system.
Entanglement entropy provides insights into the complexity and correlations present within a quantum system. It reveals the amount of entanglement shared between different subsystems. It is crucial for understanding quantum phenomena such as quantum teleportation and quantum computing.
The Universal Significance of Entropy
Entropy carries universal significance beyond its applications in specific branches of physics. Let’s look at the broader implications of entropy in understanding the arrow of time, the universe, and the intriguing concept of Maxwell’s demon.
Entropy and the Arrow of Time
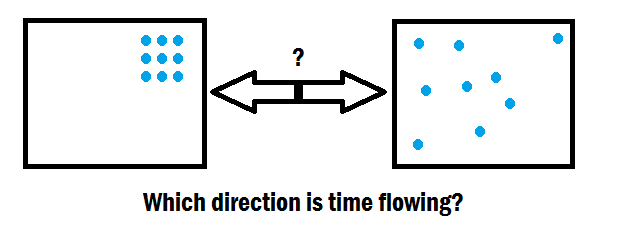
Entropy plays a crucial role in understanding the arrow of time, which refers to the asymmetry between the past and the future. The second law of thermodynamics says that an isolated system’s entropy tends to increase or remain constant over time. This implies that natural processes tend to move to higher entropy. This results in an increase in disorder and randomness.
The arrow of time has various entropy concepts, making it very related because, in a macroscopic sense, the past has lower entropy than the future. It is much more probable to observe a shattered glass returning to its original form (low entropy) than to witness a shattered glass spontaneously assembling itself (highly unlikely due to the increase in entropy).
Entropy and the Universe
Entropy also provides insights into the evolution and fate of the universe itself. According to the concept of cosmic entropy, the universe began in a state of low entropy, such as the Big Bang, and has been increasing in entropy ever since.
As the universe expands and cosmic structures form, entropy continues to increase. This leads to a gradual dissipation of energy and a move towards a state of maximum entropy known as the heat death of the universe. In this scenario, all usable energy is evenly spread out, and no further work can be done.
Maxwell’s Demon and the Perpetual Motion Machine
Maxwell’s demon is a thought experiment that challenges our understanding of entropy and its relationship to energy. The demon is a hypothetical being that can selectively allow high-energy particles to pass through a gate while preventing low-energy particles from passing.
If the demon could exist and operate without expending any energy, it would seemingly violate the second law of thermodynamics by creating a perpetual motion machine that produces useful work without any energy input. However, the resolution lies in the increase in entropy associated with the demon’s information processing and memory. The demon’s actions ultimately lead to an increase in overall entropy, ensuring that the second law of thermodynamics is not violated.
Conclusion
In conclusion, to understand the universe’s behavior and the chaos that exists, we must understand what is entropy in physics. Entropy in physics is a fundamental concept in understanding the behavior of the universe. It applies to everything from the microscopic realm of particles to the grand expanse of cosmic structures. Its significance spans various branches of physics, from thermodynamics to quantum mechanics, highlighting its pervasive role in defining the nature of systems, energy distribution, and the direction of natural processes. However, even thought entropy in physics has a lot of use cases, we use entropy in other disciplines other than entropy, too. Wherever we use it, entropy is a measure of disorder and randomness in a system. The second law of thermodynamics states that entropy in isolated systems always increases, defining the arrow of time.
The implications of entropy extend beyond physics. Its association with information theory provides a framework to comprehend uncertainty and randomness, while cosmic entropy traces the evolution of the universe from a state of low entropy towards an eventual heat death characterized by maximum entropy. The intriguing conundrum presented by Maxwell’s demon challenges our understanding of entropy’s relationship with energy, ultimately affirming the law of increasing entropy even in such hypothetical scenarios. Entropy is not only a physical principle but also a profound concept that shapes our understanding of the fundamental workings of the universe.